✅ ピグマリオンとは?数字や図形を通して思考力を育てる教育法
ピグマリオンとは、幼児から小学生を対象とした数学的能力を向上させるメソッドです。単なる計算や暗記ではなく、「指先能力」をスタートとして「空間認識力」「数量感覚」「論理的思考力」を育むことに重きを置いています。
特に、数と図形を結びつけて考える力、目に見えない関係性をイメージする力は、後々の中学・高校数学に直結します。
✅ 反転・対称移動のような「幾何的操作」が得意になる理由
たとえば中学数学で登場する「図形の対称移動」や「点対称・軸対称」「座標変換」などは、単なる作業ではなく、空間的なイメージ力と抽象的思考が求められます。
📌 ここで活きるのがピグマリオンで培った力
ピグマリオン教育では、以下のような教材・課題が登場します:
- 点描写や図形の写し取り
- 立体の展開図・折りたたみのイメージ
- 図形の回転・反転・重ね合わせ
- 「いくつ分?」「どのくらい?」といった量の分割と統合
これらの経験があると、
「この図形をy=xに関して対称にしたらどうなる?」
「この点を座標でどう表せる?」
といった問題に対し、イメージを持って代数的に処理することがスムーズになります。
✅ ピグマリオンで身につくのは「算数力」ではなく「数学に活きる力」
多くの保護者が「うちの子、計算は得意だけど図形が苦手で…」と悩まれます。
ですが、図形力・空間認識力はトレーニングで確実に伸びます。そして、ピグマリオンが目指しているのは「単なる計算の速さ」ではなく、
- 問題を図として捉える力
- 複雑な情報を抽象化して整理する力
- 頭の中で操作・変換する力(=数と形の感覚)
これらは、**高校数学や物理、さらにはプログラミングや工学分野にもつながる“思考力”**です。
✅ 実例:「ピグマリオンで学んだ子が座標変換を得意にする理由」
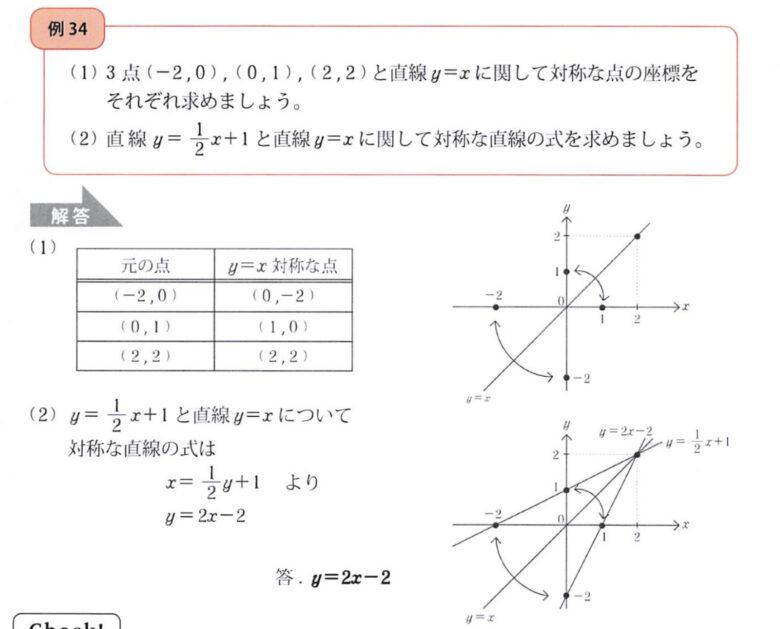
中学の数学で登場する「点 (x, y) を直線 y = x に関して対称に移す」という問題。
これは数学的には「xとyを入れ替える」という代数操作ですが、ピグマリオンで図形を自由に回転・反転してきた子どもたちにとっては、
「ああ、これはこの向きでひっくり返るね」
というイメージ→式変換のルートが自然にできています。
これは単なる知識ではなく、幼児期からの図形感覚の積み重ねによるものです。
✅ カリキュラムが早く終わる子は、小学生のうちに「中学数学」を理解できる
ピグマリオンのカリキュラムは、年齢ではなく理解度ベースで進むのが大きな特徴です。
そのため、図形や思考系の課題に強い子どもは、小学校中学年の段階で小学生内容を修了し、中学数学の範囲に入っていくことも珍しくありません。
1割くらいのお子様は、
- 小2でで合同・相似や立体の切断を直感的に理解する
- 小3で反比例や座標移動の問題を解いている
という進度です。

幾何的操作(反転・対称移動)を代数的に処理する力を養い、麻布十番教室に限らず、ピグマリオンのお教室に通室している子どもたちは、中学受験においても図形・思考問題を武器にし、トップレベルの学校に上位合格するケースが多数あります。
幾何的操作(反転・対称移動)を代数的に処理する能力を小学校中学年から養えば、テクニックや解法暗記だけに頼る必要がなくなります。
ピグマリオンで育てた「見える力」「つなげる力」「ひらめく力」は、単なる受験テクニックではなく、自ら考え抜く本物の学力となって表れるのです。
✅ ピグマリオンの図形センスは、数学の土台になる
算数から数学へとステップアップしていく上で、計算力や公式の暗記だけでは限界があります。
- 「なぜこの式になるのか?」
- 「この操作は何を意味しているのか?」
といった“意味理解”があってこそ、本当の学力が育ちます。
ピグマリオンの図形トレーニングは、この「意味」をイメージで捉える力を育てる点で、まさに数学の土台をつくっていると言えるでしょう。
✅ まとめ:ピグマリオンで育まれた力は、未来の数学・科学の力になる
ピグマリオンで育つ力は、単なる「先取り学習」ではありません。
図形センス、空間把握、数量認識、思考力――これらは中学・高校・大学と進むにつれ、数学の真の力として開花します。
そして、カリキュラムを早めに修了するような子どもたちは、小学生のうちから中学数学に触れ、中学入試でも上位校に合格できるだけの深い学力と柔軟な思考力を手に入れていくのです。
だからこそ、幼児期の「見る・感じる・操作する」経験を大切にするピグマリオンは、将来の数学的思考力の育成にとって、極めて有効な教育法なのです。
