前回は、「円周率が3.05より大きいことを証明せよ。」という2003年の東大の数学の過去問をもとに、「数を強化するためのベクトルを間違えないでください」という記事を書きました。
今回も、それと似たような内容になりますが、ピグマリオン学院に通っていただく方の保護者の皆様とは、最低限の価値共有をしていきたいため、
・なぜ、10000までのたし算、ひき算ができることを重視しているか?
・なぜ、先取りで「かけ算九九を暗記しないでください」とお伝えしているのか?
ということを、何度もお伝えしていきたいと思います。
ただし、ピグマリオンでは、
「子どもであれ、保護者であれ、講師側は教えることはできない。お伝えして、ご自身で考えていただく」
というスタンスです。
選択するのは、皆様です。私たちは押し付けることはできません。
さて、円周率の証明問題が出された4年前の1999年、東大では以下のような問題が出題されました。
(1)一般角θに対して、sinθ、cosθの定義を述べよ。
(2)一般角α、βに対して、次の式を証明せよ。
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ
(東京大 1999)
こちら、数学の世界からしばらく離れているとピンと来ない方もいるかもしれませんが、一言で説明すると、
「加法定理を証明せよ」
という問題です。
加法定理は、三角関数の中でも、最も重要な公式として覚えている方も多いかと思いますが、その中でも重要なのが、
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ
とされています。東大はこの公式の証明を受験問題として出題したのですが、正答率は非常に低かったということで、東大受験生の中でも「盲点」だったようです。
この出題が何を意味しているかというと、
「あなたがフル活用しようとしていたその公式、本当にその意味が分かって使用していますか?」
「本質を理解する学びをしてきましたか?」
という出題者の意図は明確です。
もちろん、このような問題を捨て問にして、
「暗記数学で得た知識を活用して、取れる問題だけ拾っていく」
という選択で、合格した方々はたくさんいたに違いありません。
ただ、例えば、こちらの問題が20点の配点だったとすると、この問題が解答できたのとできなかったのとでは、かなり大きな差がついたことは確かでしょう。
さて、一度前回の記事と同様に、ここで改めて問います。
こちらの問題を解くのに、必要なのは計算力ですか?
低学年での計算のスピードは必要ですか?
そろばんやくもんでの経験が役に立つと思いますか?
フラッシュ暗算の能力は必要ですか?
そもそも、そろばんやくもんをしなくても、高校数学まで教科書+αのレベルで学んでいけば、大学受験に耐えうる計算力はついていきます。
幼児や低学年で、数量感が養われずに先取りした計算力や計算スピードは、成長ともに差が縮まっていきます。
幼児期に暗記した日常生活で活用されない知識は、使用しないものは忘却していきます。
一方、幼児から養われる「思考力=自分で解決する能力」は、その後の人生に大きく生かされていきます。
また、思考力を形成する大きな要素である図形能力は、幼児期が最も伸びる時期であるため、小学校中学年からの学び始めでは遅すぎる可能性があります。
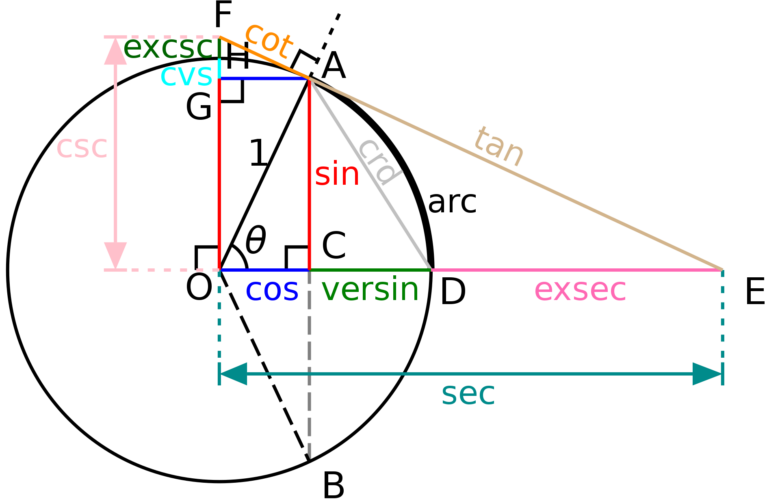
図形感が養われて入れば、三角関数なども、図形的なイメージで関係性を捉えることができる可能性が高まります。
一方、図形感が養われないまま丸暗記型で積み重ねていくと、公式の文字列を丸暗記するか語呂合わせなどで覚えるようになる可能性が高まります。
幼児期のかけ算九九の先取りに関しては、まさに文字列の丸暗記の要素が強いのが特徴です。
小学校に入ってからであれば、例えば授業の中で副教材としてブロックを使ったりして、多少なりとも数量感とともに九九を暗記するような要素が入っている場合もあります。
しかし、その要素をマルッとすっ飛ばしてしまいがちなのが、幼児期のかけ算九九暗記の特徴でもあります。
式と図形を切り離して考える幼児期の癖が、その後に悪影響を及ぼす可能性がある
そのリスクをうまく回避できれば良いとは思いますが、ピグマリオンをご存知の皆様は、あえてそのような道を選択する必要もないと考えています。
ピグマリオンでの取り組みにより、数量感覚が養われ、図形能力が養われ、その延長で計算能力が高まる。
当然ながら、かけ算も、それまでの加減計算やその他のピグマリオンでの取り組みで獲得してきた能力を生かして、暗記せずにできるようになる。
ドット棒Cを生かせば、図形的な認識も容易にできる。
3×8 = 3×10-□
という問題を見たときに、
「3のドット棒を2本取れば良いから6」
という図と式と解答が一瞬で浮かび上がるようになるのです。
これが、かけ算九九から覚えたお子さまだと、
「3かける8は24で、3かける10は30、30は24よりも6大きいから、6」
と、どうしても計算しないと答えを求められなくなります。
上記の問題、どちらのアプローチの方が早く解けると思いますか?
答えは、聞くまでもないかと思います。
それなら、「計算が速い」とは、なんなのでしょうか?
全てを一対一対応で覚える、暗記する、というのは、本来の算数や数学の世界からはかけ離れた世界です。
ある意味、大学受験合格のためだけに「弱者の方法」として「暗記数学」をするのであれば、それはそれで一つの考え方かもしれません。
ただ、親として「暗記数学」という選択につながりやすい「暗記算数」の世界にお子さまを小さい頃からどっぷりと浸からせて良いのでしょうか?
お子さまの思考力の可能性を狭めるリスクはないのでしょうか?
幼児期のそろばんの学びは、加法定理の証明ができるお子さまに近づきそうですか?
幼児期のくもんの学びは、加法定理の証明ができるお子さまに近づきそうですか?
お子さまの思考法の根本に影響する可能性があるお話のため、重ねて記事として掲載いたしました。
ピグマリオン学院 麻布十番教室
