前回は、小学3年生以下を対象にした算数オリンピックのカテゴリーである「キッズBEE」の三面和の問題について記事にしましたが、今回は筑波大学附属駒場中の2010年の過去問を紹介します。
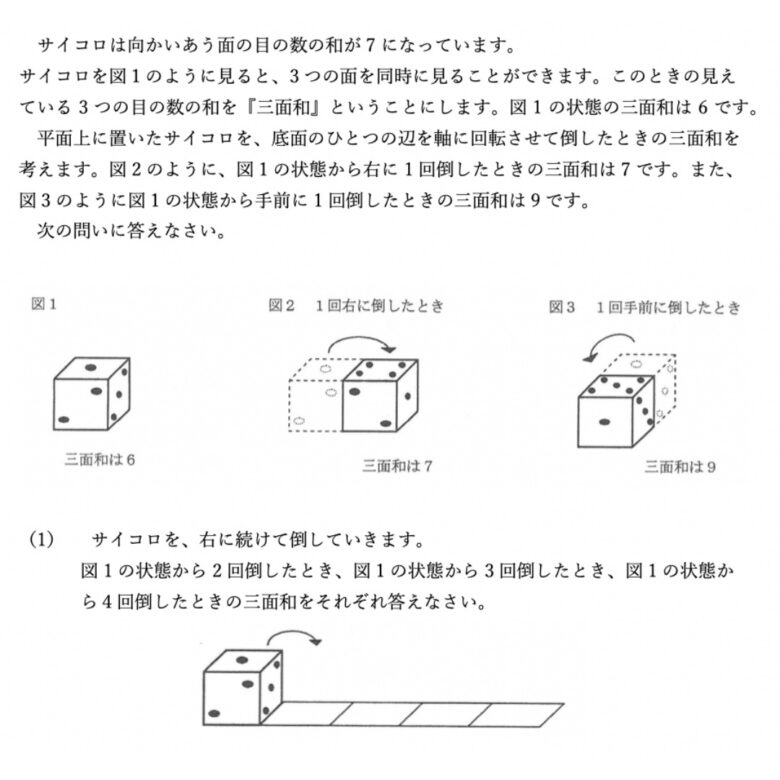
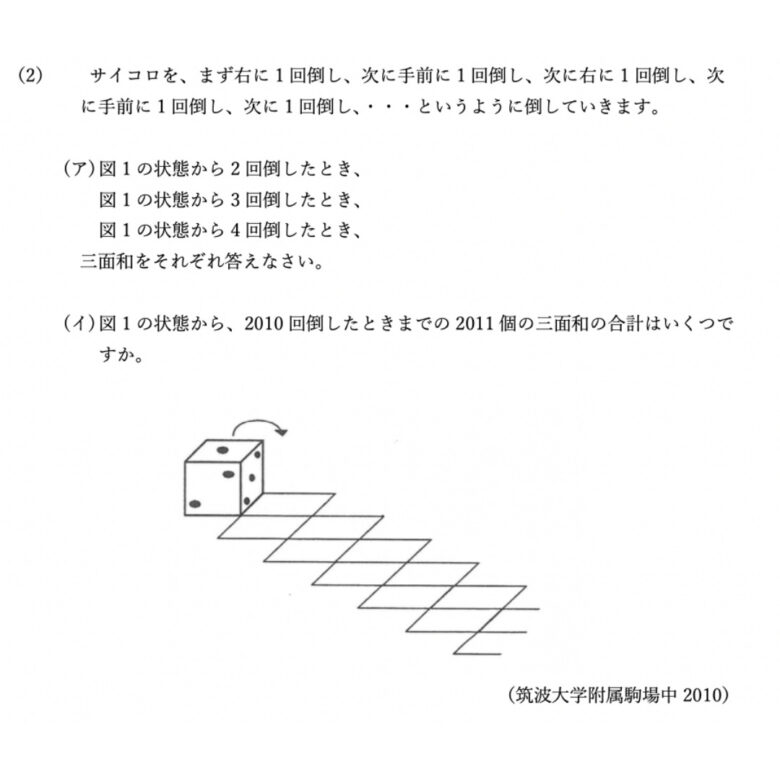
こちらの問題も、ピグマリオンに取り組んでいるお子さまであれば、(2)の(イ)以外の問題は、小学生低学年で素早く解けると思いますし、(2)の(イ)の問題も、高学年のお子さまはラッキー問題だと言えます。
ピグマリオン学院であれば、Mグレード(年長相当)から実施するサイコロころころや、その他の立体認知能力を高める取り組みで、
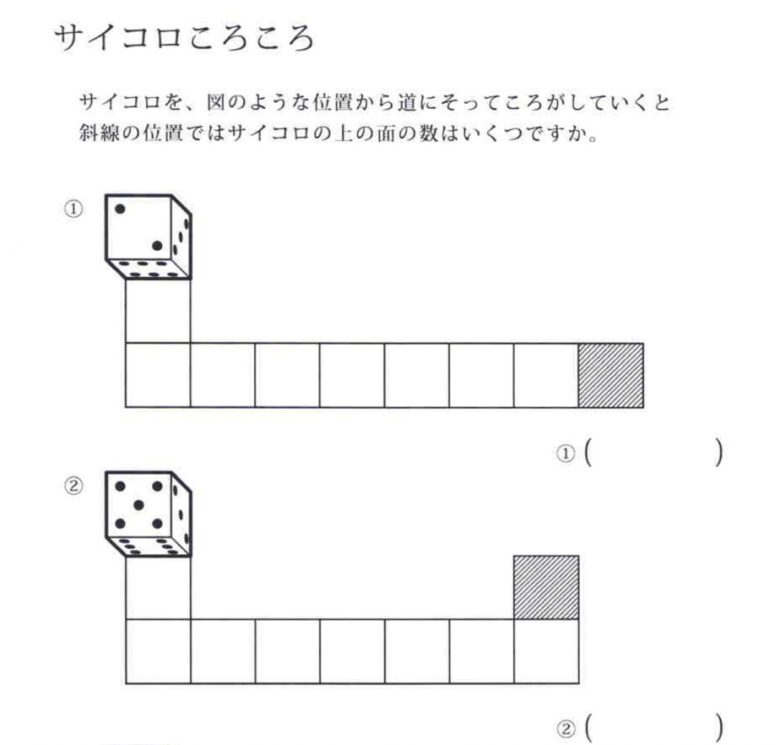
脳内でサイコロが転がるイメージがあれば、このような問題はすぐに解答できます。
また、たまに解説にある「サイコロを潰して考える」という解き方は、
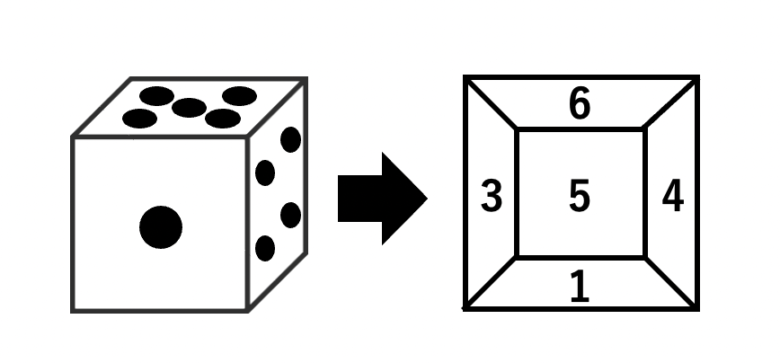
個人的には時間もかかり非効率だと思います。
いわゆる受験テクニックなのかもしれませんが、自らこのような解答方法を編み出したお子さま以外は、将来のお子さまの何の役にも立ちません。
テクニックになるべく頼る必要の無いような”図形感覚”を幼少期から身につければ、
「自分自身で解法を生み出していく」
という経験を、受験勉強を通じて得ることができるかと思います。
例えば(2)の(ア)の3回倒したときの状態は、図1の「1+2+3=6」が見えていた状態と裏返した状態になることに気づき「4+5+6=15」と即答できるお子さまは、サイコロころころを続けていく中で、自ら「規則性」を創造したのだな、と思います。
(2)の(イ)の問題については、試行錯誤をする中で、「7→10→15→14→11→6」という6つの数字の周期が335回続くという法則を導き出せるかとは思いますが、なぜ6つの周期になるかというと、立方体の展開図の連続だから”335個のサイコロがあるのと同じことなのだな”、というところに気付けたりすると、
「この子は、解答や結果だけではなく、問題の本質をパッと見抜く力がある」
ということもわかります。
直感的に本質を察知するような能力は、社会に出てからも役に立つ能力になるはずです。
このように、東京の最難関校である筑波大学附属駒場中の算数の問題も、ピグマリオンにかかれば低学年で解ける問題があるということを、改めて認識していただき、
「幼児期は、とにかく計算の先取り」
という方針に偏り過ぎないで欲しいと感じます。
ピグマリオン学院 麻布十番教室
解答
(1)2回:12(2,6,4)
3回:11(2,3,6)
4回:6(2,1,3)
(2)(ア)2回:10(4,5,1)
3回:15(4,5,6)
4回:14(3,6,5)
(イ)21111
(最初の三面和「6」のあとは、「7→10→15→14→11→6=63」が335回続く→6+63×335)

